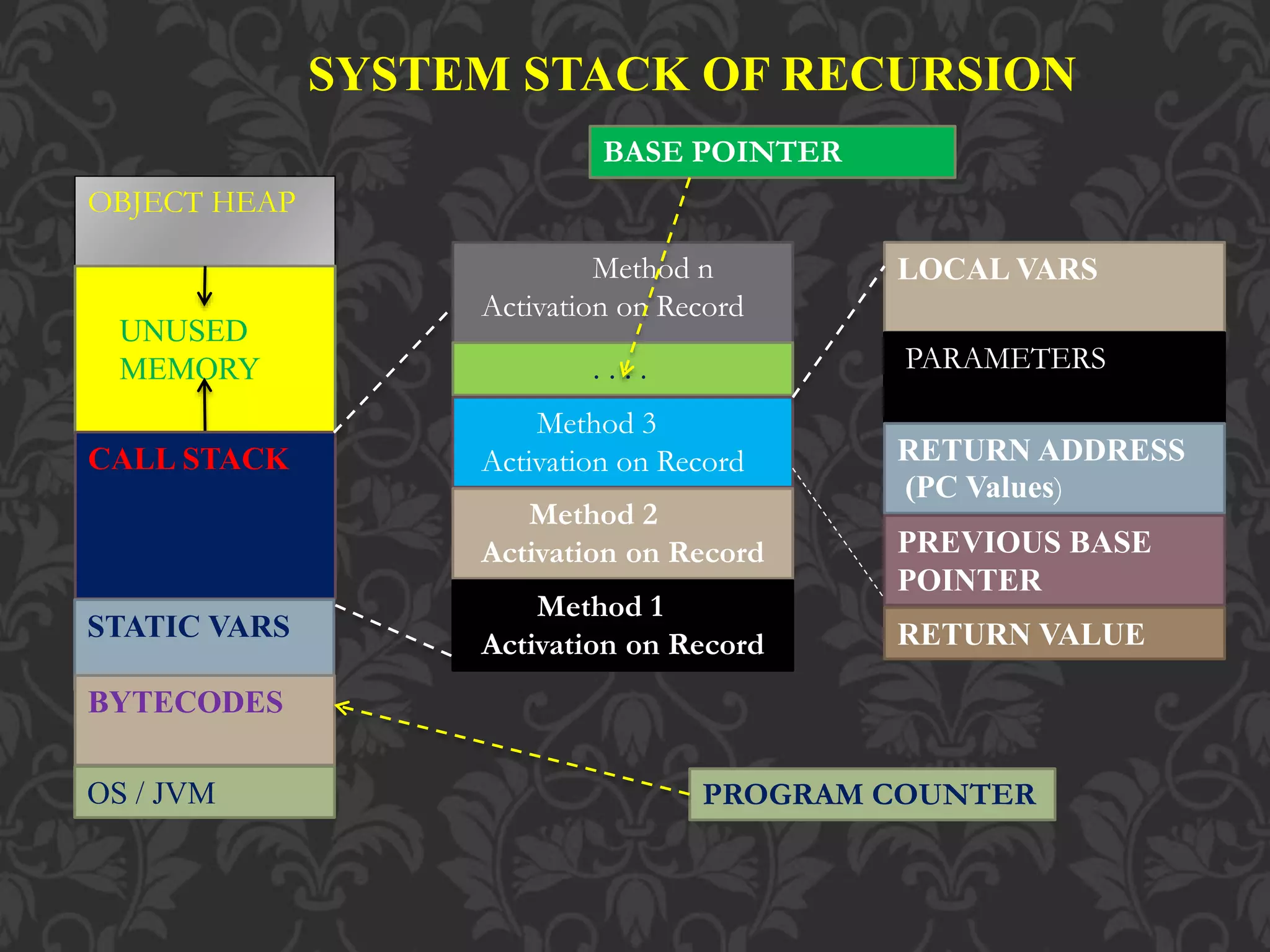
The document discusses recursion, which is when a function calls itself. It provides examples of recursive algorithms, types of recursion including single, multiple, direct, indirect, anonymous, and structural recursion. It also discusses recursive functions like the factorial function, tail recursion, and mutually recursive functions. Additionally, it covers recursive data types, the order of execution in recursive functions, and how recursion uses the call stack in memory.