Download to read offline
Understanding K-Nearest Neighbor (KNN) Algorithm
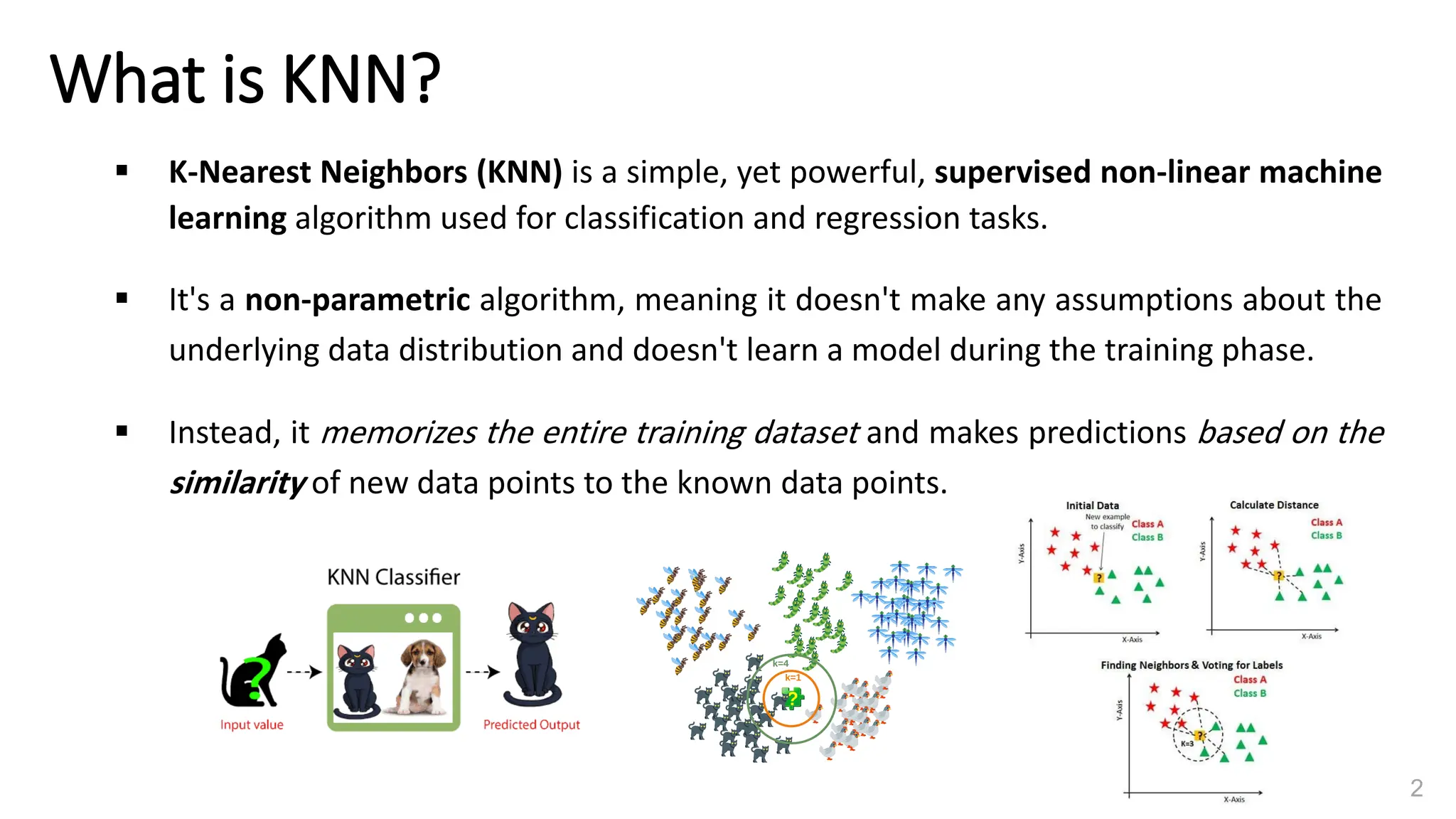
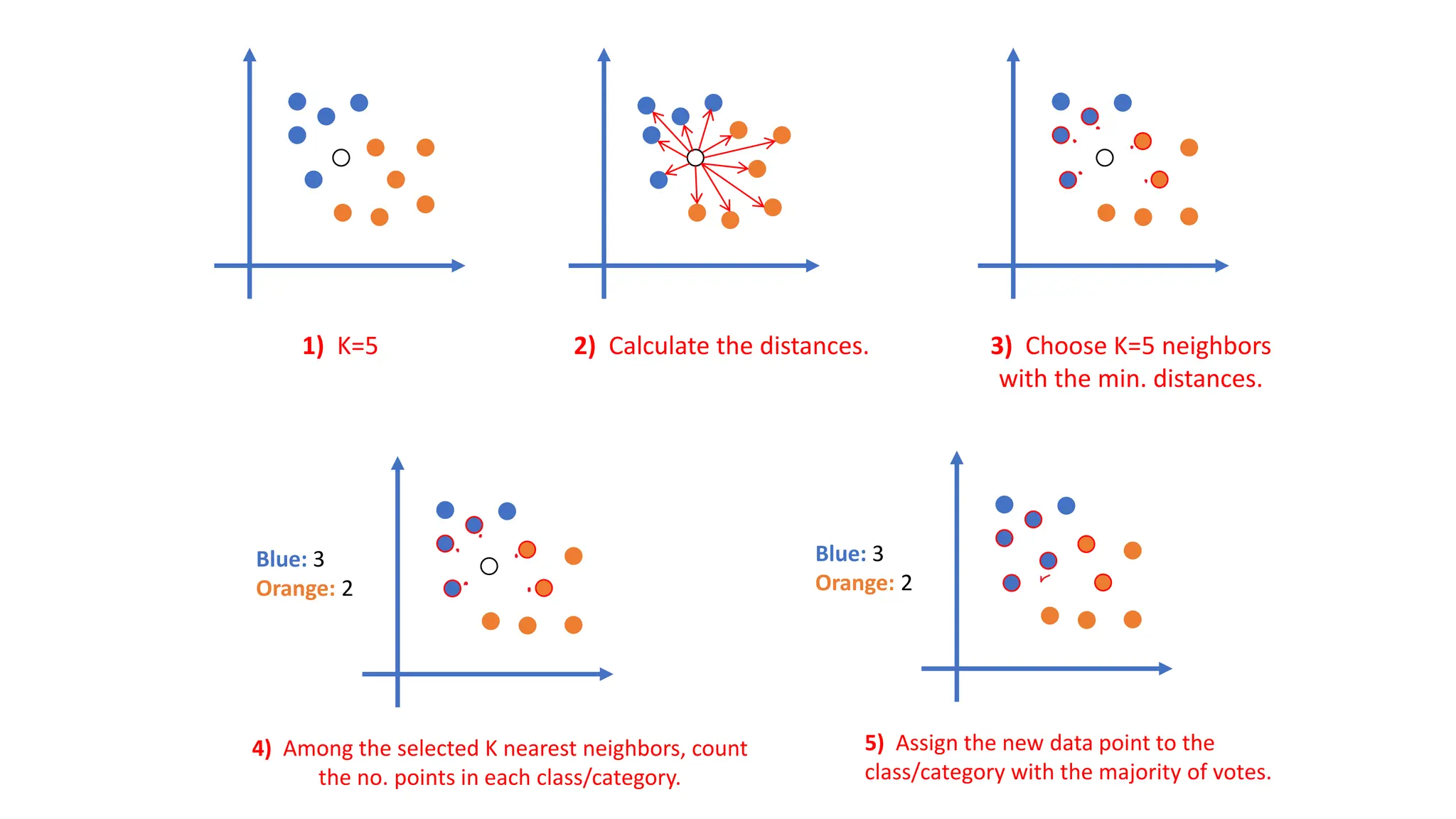
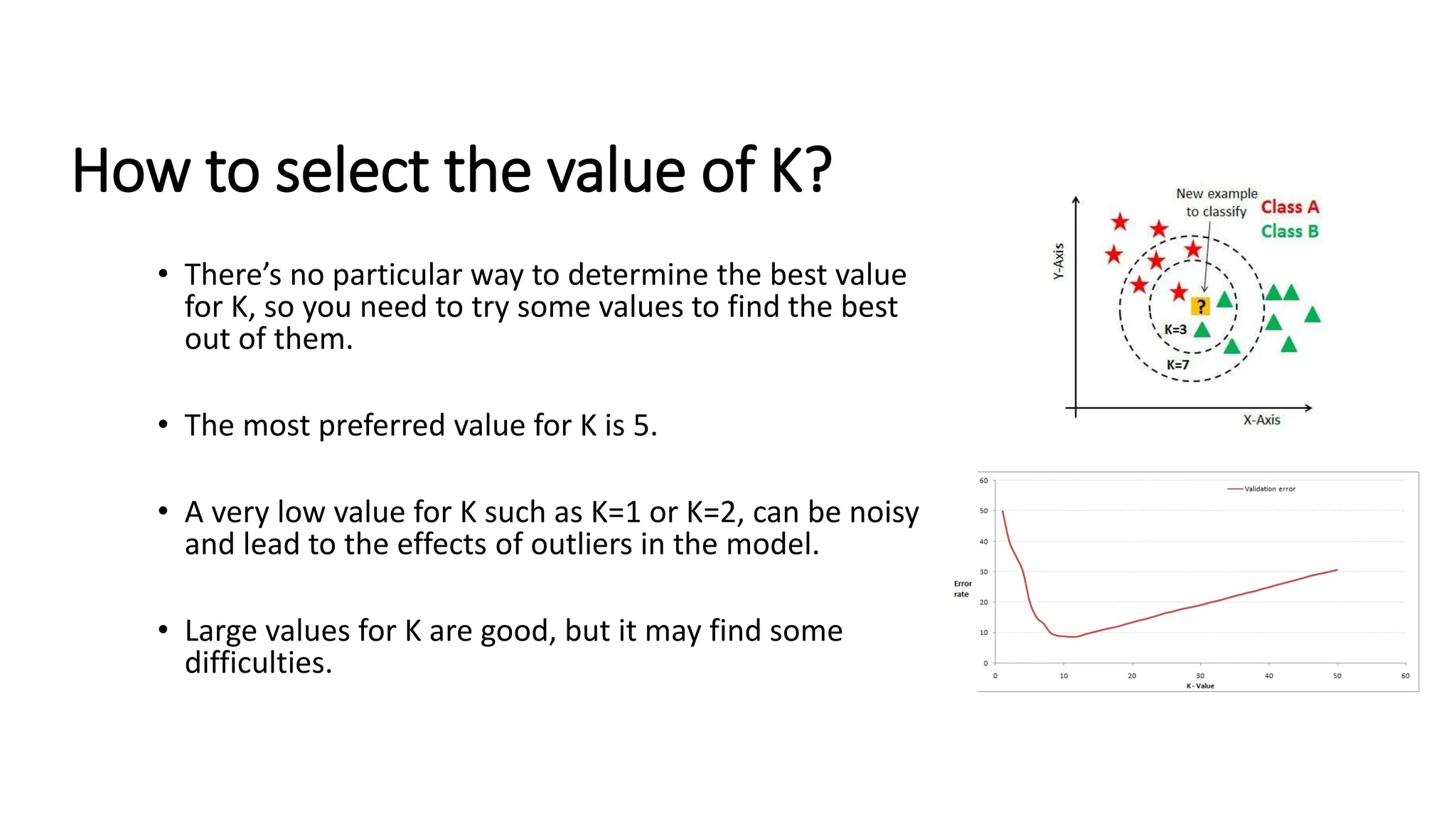
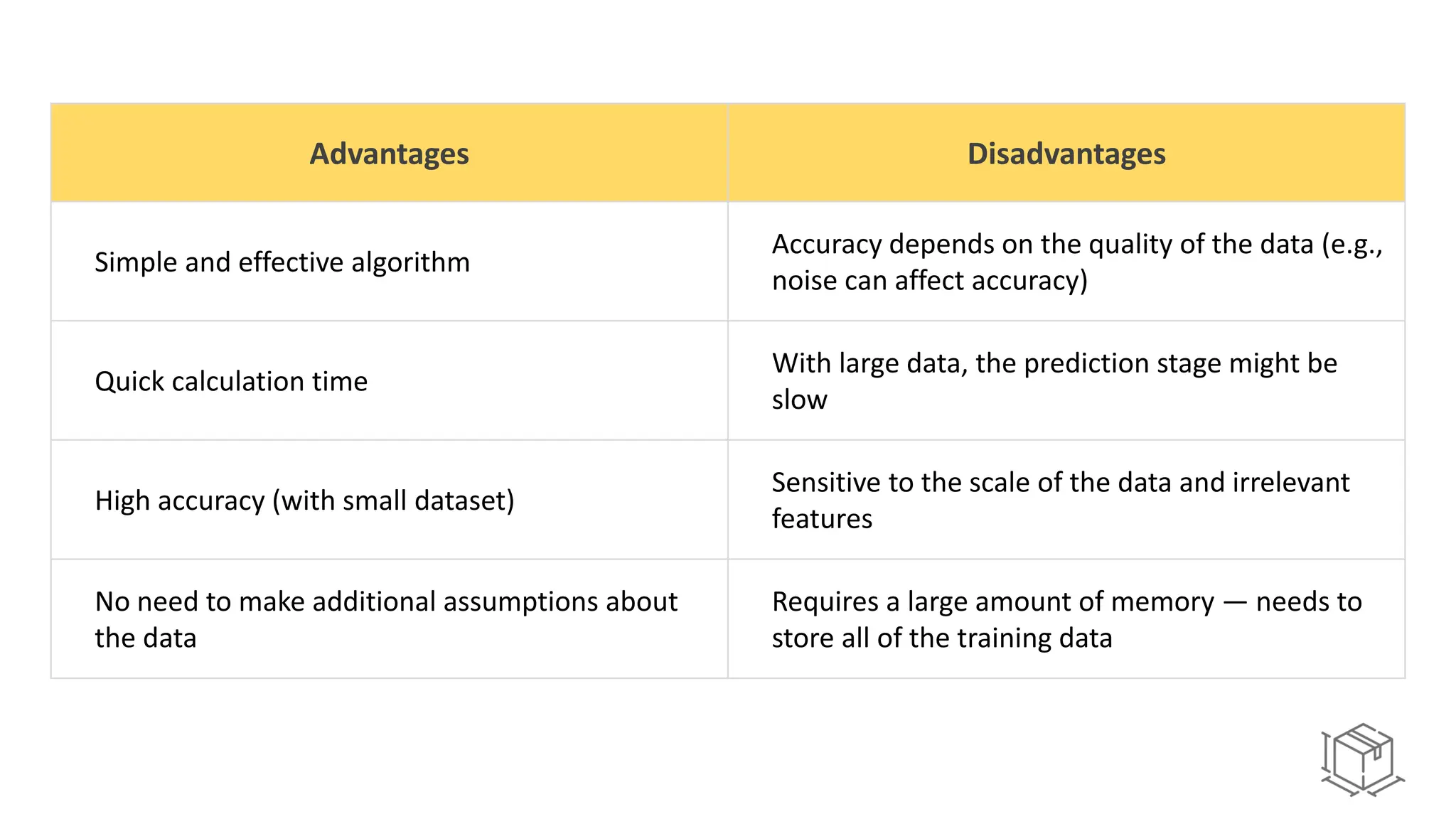
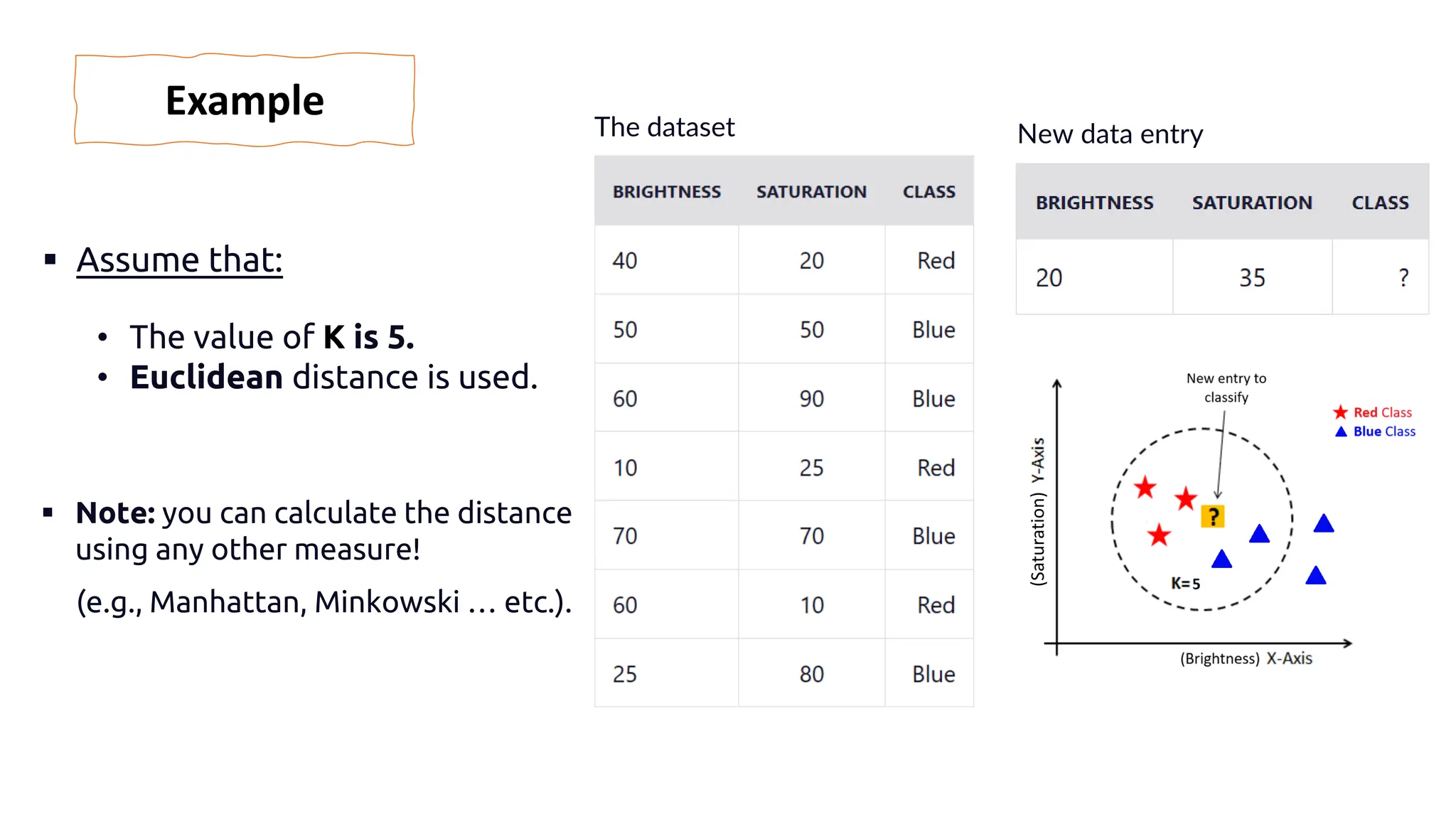
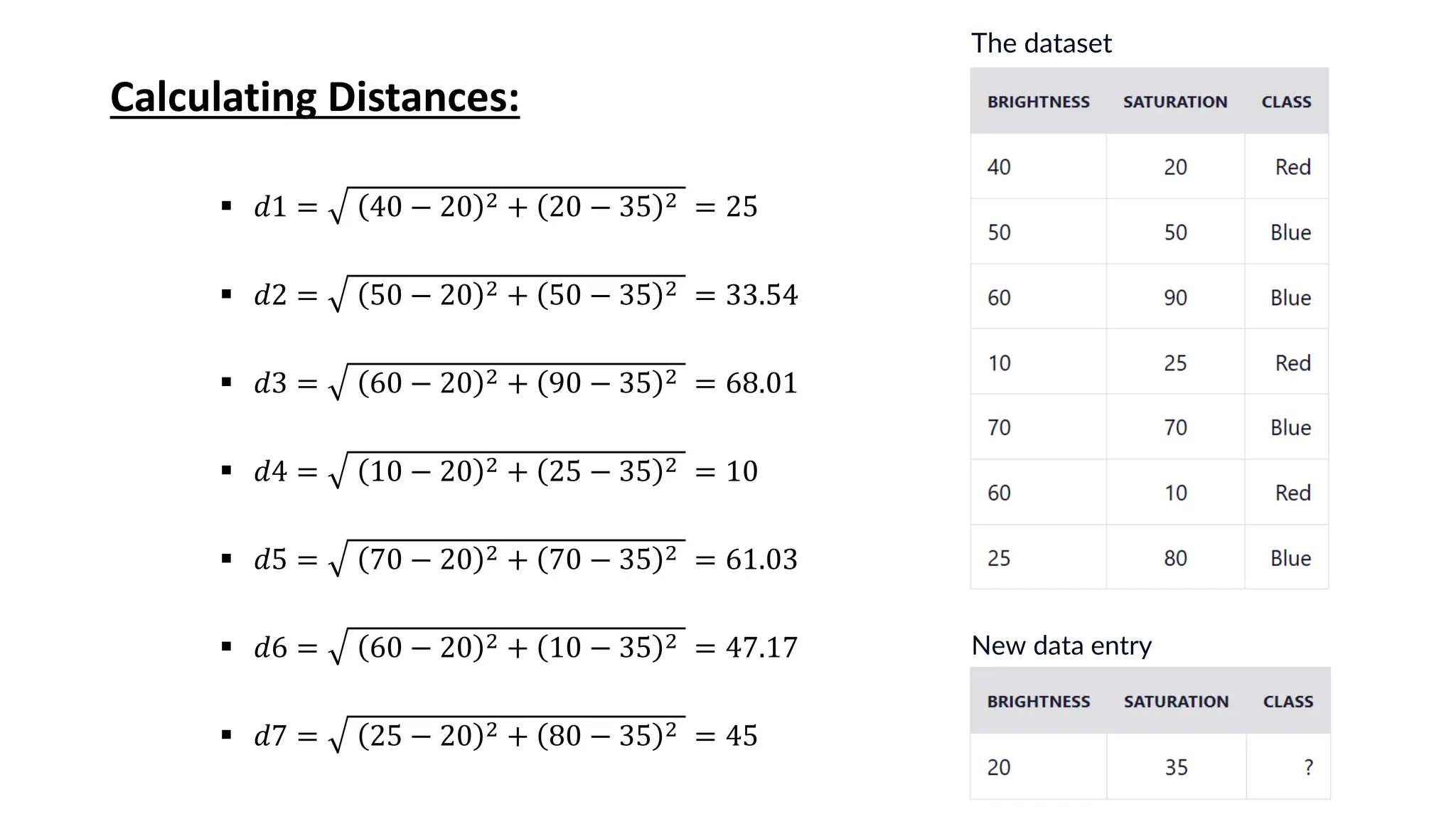
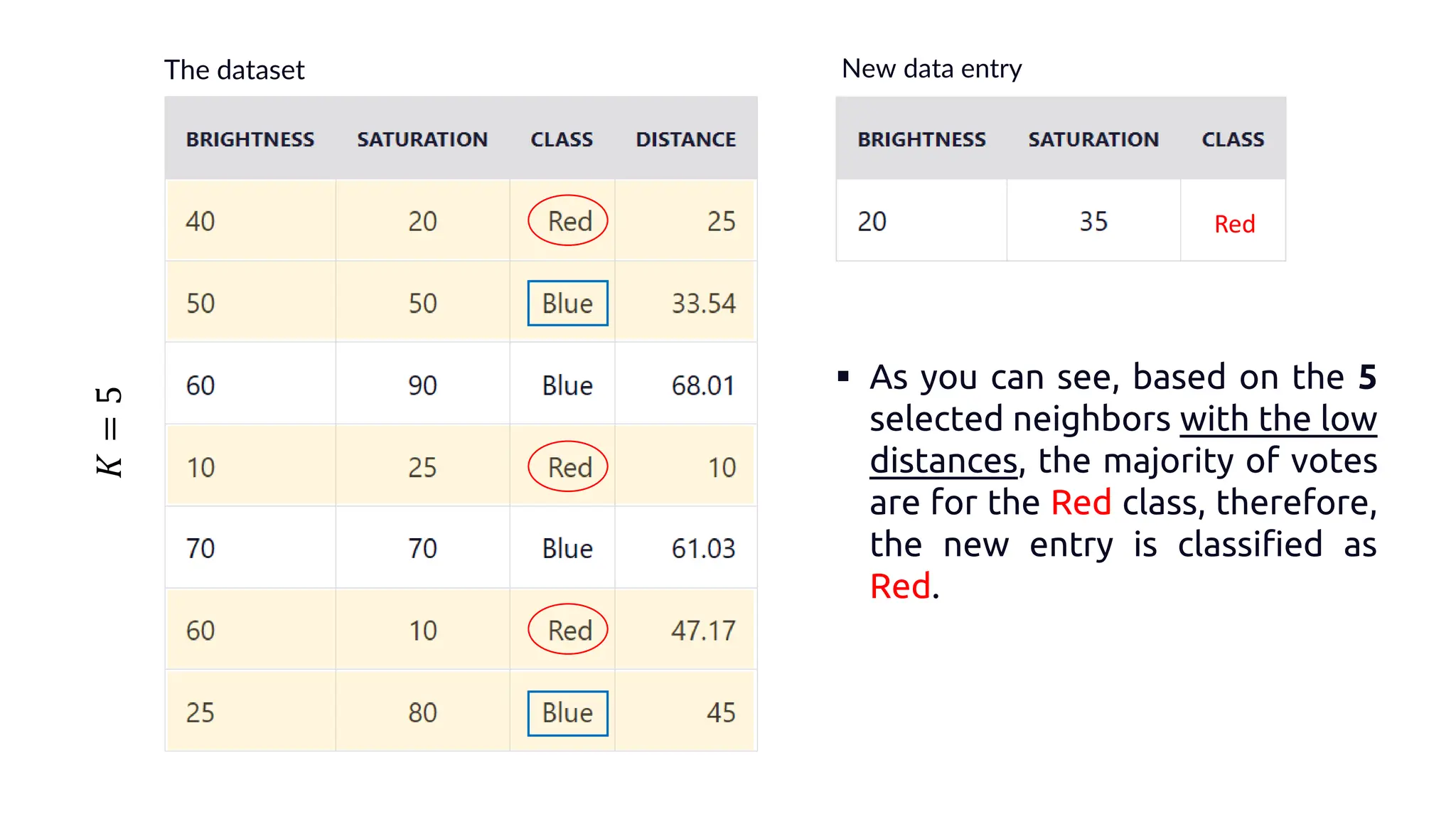
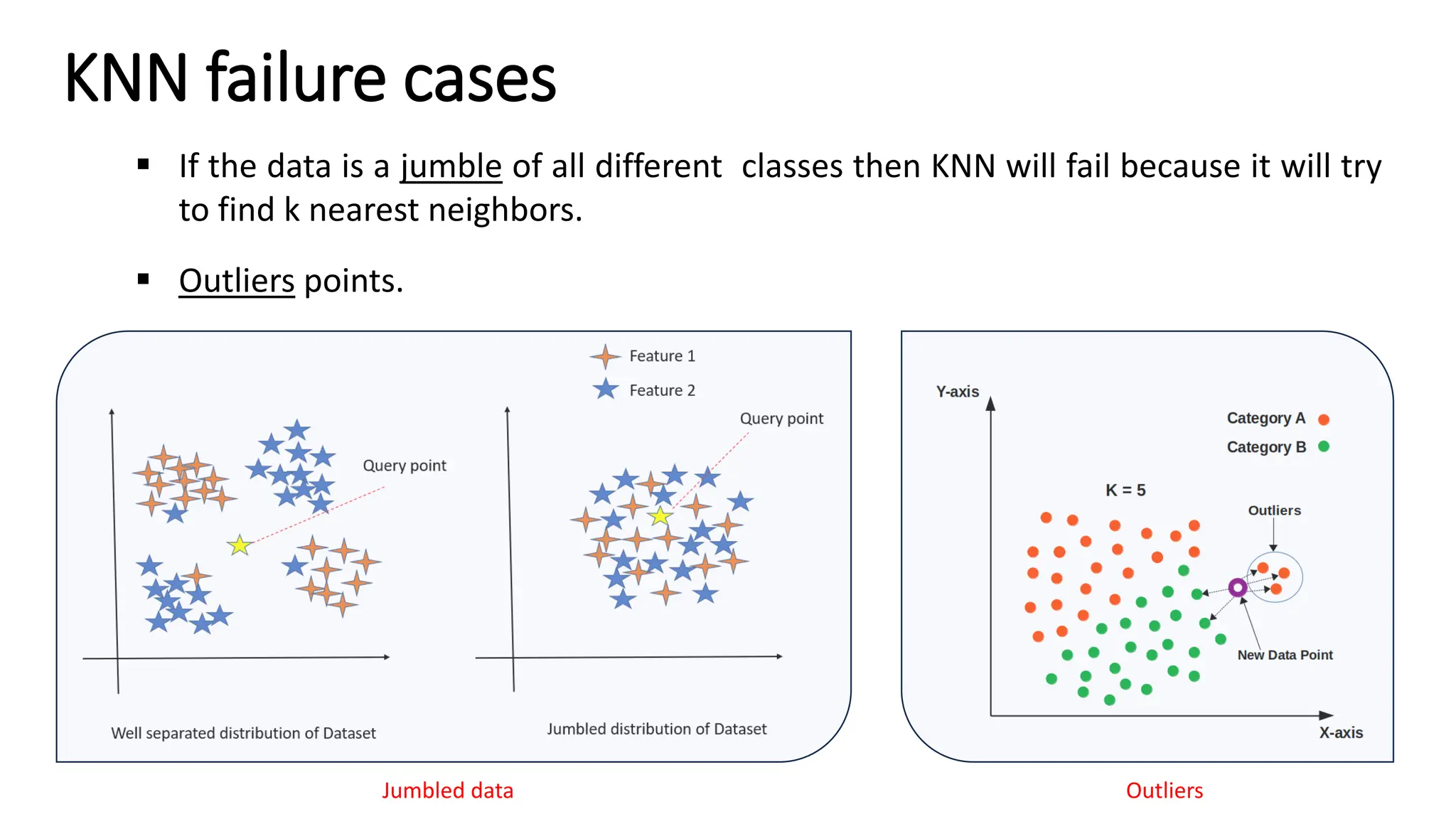
The document explains k-nearest neighbors (k-nn), a supervised machine learning algorithm used for classification and regression, detailing its workings and structure. Key steps in the k-nn process include selecting the number of neighbors (k), calculating distances, and classifying new data points based on the majority vote of the nearest neighbors. It also discusses advantages and disadvantages, such as simplicity, sensitivity to data quality, and memory requirements.
Understanding K-Nearest Neighbor (KNN) Algorithm
- 1.
- 2. Agenda ▪ What isK-NN? ▪ How does K-NN work? ▪ K-NN algorithm and structure ▪ Advantages of K-NN ▪ Disadvantages of K-NN ▪ Example 1
- 3. ▪ K-Nearest Neighbors(KNN) is a simple, yet powerful, supervised non-linear machine learning algorithm used for classification and regression tasks. ▪ It's a non-parametric algorithm, meaning it doesn't make any assumptions about the underlying data distribution and doesn't learn a model during the training phase. ▪ Instead, it memorizes the entire training dataset and makes predictions based on the similarity of new data points to the known data points. What is KNN? 2
- 4. ▪ Step-1: Selectthe number K of the neighbors. ▪ Step-2: Calculate the distance of K number of neighbors. ▪ Step-3: Take the K nearest neighbors as per the calculated distance. ▪ Step-4: Among these K neighbors, count the number of the data points in each category. ▪ Step-5: Assign the new data points to that category for which the number of the neighbor is maximum. How does KNN work? (Algorithm) 2
- 5. 1) K=5 2)Calculate the distances. 5) Assign the new data point to the class/category with the majority of votes. Blue: 3 Orange: 2 3) Choose K=5 neighbors with the min. distances. 4) Among the selected K nearest neighbors, count the no. points in each class/category. Blue: 3 Orange: 2
- 6. Minkowski Distance (Named afterthe German mathematician, Hermann Minkowski) Manhattan Distance (Also called taxicab distance or cityblock distance) Euclidean Distance (The shortest distance between any two points) 𝑝 = 1 𝑝 = 2 Ways to calculate the distance in KNN
- 7. How to selectthe value of K? • There’s no particular way to determine the best value for K, so you need to try some values to find the best out of them. • The most preferred value for K is 5. • A very low value for K such as K=1 or K=2, can be noisy and lead to the effects of outliers in the model. • Large values for K are good, but it may find some difficulties.
- 8. Advantages Disadvantages Simple andeffective algorithm Accuracy depends on the quality of the data (e.g., noise can affect accuracy) Quick calculation time With large data, the prediction stage might be slow High accuracy (with small dataset) Sensitive to the scale of the data and irrelevant features No need to make additional assumptions about the data Requires a large amount of memory — needs to store all of the training data
- 9. New data entry Thedataset ▪ Assume that: • The value of K is 5. • Euclidean distance is used. Example ▪ Note: you can calculate the distance using any other measure! (e.g., Manhattan, Minkowski … etc.). (Saturation)
- 10. The dataset Calculating Distances: ▪𝑑1 = 40 − 20 2 + 20 − 35 2 = 25 ▪ 𝑑2 = 50 − 20 2 + 50 − 35 2 = 33.54 ▪ 𝑑3 = 60 − 20 2 + 90 − 35 2 = 68.01 ▪ 𝑑4 = 10 − 20 2 + 25 − 35 2 = 10 ▪ 𝑑5 = 70 − 20 2 + 70 − 35 2 = 61.03 ▪ 𝑑6 = 60 − 20 2 + 10 − 35 2 = 47.17 ▪ 𝑑7 = 25 − 20 2 + 80 − 35 2 = 45 New data entry
- 11. The dataset Newdata entry 𝐾 = 5 ▪ As you can see, based on the 5 selected neighbors with the low distances, the majority of votes are for the Red class, therefore, the new entry is classified as Red. Red
- 12. ▪ If thedata is a jumble of all different classes then KNN will fail because it will try to find k nearest neighbors. ▪ Outliers points. KNN failure cases Jumbled data Outliers
- 13.