I'm a bit new to the application, and I'm not sure how to draw a parallelepiped in Mathematica.
$\begingroup$ $\endgroup$
0 
Add a comment |
1 Answer
$\begingroup$
$\endgroup$
After version 9: Parallelepiped.
Graphics3D[Parallelepiped[{0, 0, 0}, {{1, 0, 0}, {1, 1, 0}, {0, 1, 1}}]]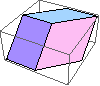 
Version 9 or before. Right from the documentation of ShearingMatrix, that is a GeometricTransformation:
Graphics3D[{GeometricTransformation[{Opacity[.85], Red, Cuboid[]}, ShearingMatrix[Pi/4, {1, 0, 0}, {-1, 1, 0}]]}, Boxed -> False]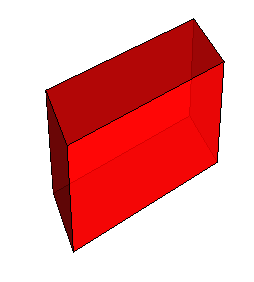 
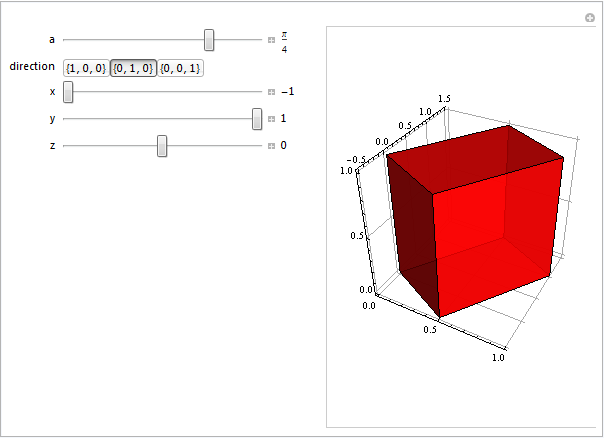
A dynamic manipulator to understand arguments:
Manipulate[ Graphics3D[{ GeometricTransformation[{Opacity[.85], Red, Cuboid[]}, ShearingMatrix[a, dir, {x, y, z}]] }, FaceGrids -> {{-1, 0, 0}, {0, 1, 0}, {0, 0, -1}}, Axes -> True, Boxed -> False, BoxRatios -> 1, SphericalRegion -> True], {{a, Pi/4}, -Pi/2, Pi/2, Appearance -> "Labeled"}, {{dir, {0, 1, 0}, "direction"}, {{1, 0, 0}, {0, 1, 0}, {0, 0, 1}}}, {{x, -1}, -1, 1, .1, Appearance -> "Labeled"}, {{y, 1}, -1, 1, .1, Appearance -> "Labeled"}, {{z, 0}, -1, 1, .1, Appearance -> "Labeled"}, ControlPlacement -> Left ] 
