Why can't I make flip-flops in logic simulators?

The circuit you show is a gated JK latch, not a flip-flop. It suffers from a flaw: with T high and clock high, the cross-coupled NAND gates form a ring oscillator. This is sometimes called the ‘race-around’ problem. The output never settles until the clock is brought back low.

This circuit is illustrative of how not to make a clocked flop. Otherwise it’s useless. An actual toggle flop will use a pair of latches in two stages, clocked on opposite levels. This is sometimes called an ‘edge-‘master-slave’ flip-flop. The variant using a trio of latches (6 gates total) is called 'edge triggered’. Either way, these don't suffer the 'race around' flaw.

More here: How is the Q and Q' determined the first time in JK flip flop?

And here: JK latch, possible Ben Eater error?

To implement an edge triggered T Flip-Flop that does not rely on gate delay timing, requires, I believe, a minimum of 6 Nand gates. The circuit below simulates fine in CircuitLab.

^{simulate this circuit – Schematic created using CircuitLab}

Edit:

Someone has commented that this circuit is not a T flip-flop because the circuit depends upon the clock alone, and does not have separate T and clock inputs.

However, when I google "T flip-flop", the very first hit that comes up for me is this which states:

The T or "toggle" flip-flop changes its output on each clock edge, giving an output which is half the frequency of the signal to the T input.

It is useful for constructing binary counters, frequency dividers, and general binary addition devices. It can be made from a J-K flip-flop by tying both of its inputs high.

and which contains the graphic:

I don't claim that this is necessarily an authoritative refutation of the claim that a T flip-flop must have separate T and clock inputs. (There is certainly a lot of misinformation about flip-flops on the interwebs. For example, the OPs circuit, shows up all over the place labeled as a T flip-flop despite the fact that it has problems described in other answers.) However, I am offering the above information as an alternative point of view to that of the commenter.

Edit2: A commenter has asked for a state diagram for the circuit. I will provide this information, but not as a diagram.

There are 4 stable states and 12 states that are transistional between stable states in normal operation.

The stable states are:

The transitions go as follows

S1 In\$\uparrow\$ N1\$\downarrow\$ N6\$\uparrow\$ N5\$\downarrow\$ S2

S2 In\$\downarrow\$ N1\$\uparrow\$ N4\$\downarrow\$ N3\$\uparrow\$ S3

S3 In\$\uparrow\$ N2\$\downarrow\$ N5\$\uparrow\$ N6\$\downarrow\$ N4\$\uparrow\$ S4

S4 In\$\downarrow\$ N2\$\uparrow\$ N3\$\downarrow\$ S1

Another issue you might (but should) run into is this: How is the Q and Q' determined the first time in JK flip flop?.

This is especially true for a T Flip-Flop.

For a T Flip-Flop with only 2 inputs, T and Clock, there is no way for the output to get into a known state in a simulation that supports 'X'.

A good simulator will shown an 'X' on both outputs, which shows that the value is unknown.

As I have mentioned in my answer, one can use synchronous or asynchronous inputs to set the output to a known state.

For reference, I've built a T Flip-Flop with asynchronous inputs using a Master Slave JK Flip-Flop, which you can simulate in your browser:

simulate this circuit - Schematic created using MultisimLive

The circuit in the original question contains 1 or more hazards or race conditions. As such, the circuit will only work properly if the delays within the circuit are properly controlled.

An asynchronous finite state machine with hazards (or race conditions) will, in general, work properly only if delays within the circuit are properly controlled. An asynchronous finite state machine without hazards (or race conditions) or with hazards which are "covered" (and hence not active) will perform properly if there is at any time only one signal which is changing, and which does not receive new inputs until the circuit has reached a stable state.

Such asynchronous finite state machines may be implemented in a number of ways, but one way to do so is with a sum-of-products combinatorial circuit with some of the outputs fed back as inputs.

In this answer, such a circuit will be shown. However, it is probably unfamiliar to many, and is certainly less familiar than other implementations of T flip-flops, such as the master-slave implementation, or the 6 nand gate implementation shown in another answer.

We start with an asynchronous finite state machine that we wish to implement:

The flow table for this state machine is given as:

We can assign variables and values to the states to give:

with the excitation table

The Karnaugh maps for Q, Y and Z are given as follows

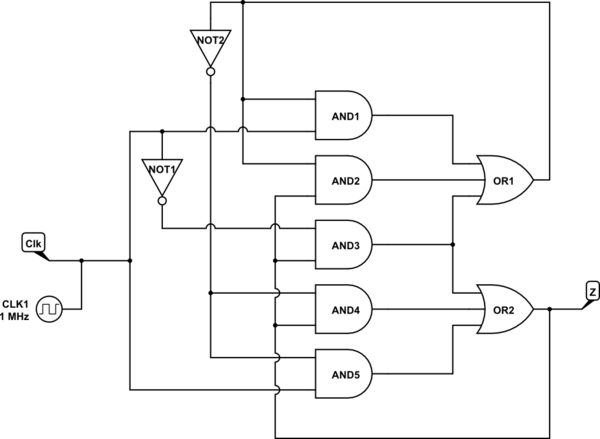
If we were attempting to find the minimal implementation of a boolean function, we would calculate a minimal sum of prime implicants that cover the function under consideration. However, such a procedure would allow our implementation to have static 1 hazards. To avoid static 1 hazards, we use extra prime implicants (in this case all of the prime implicants). This gives our combinatorial functions

\$Q = z\$

\$Y = x'z + xy + yz\$

\$Z = x'z + xy' + y'z\$

Finally, implementing this circuit as a sum of products with feedback:

^{simulate this circuit – Schematic created using CircuitLab}