32
\$\begingroup\$

I'm trying to make a quad sphere based on an article, which shows results like this:

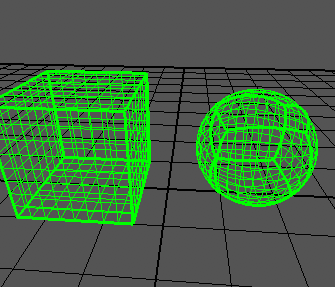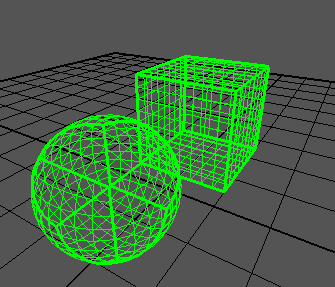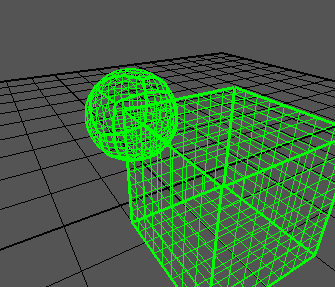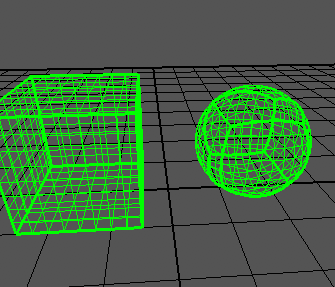
correct

I can generate a cube correctly:

before

But when I convert all the points according to this formula (from the page linked above):

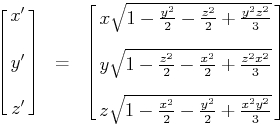
formula

 x = x * sqrtf(1.0 - (y*y/2.0) - (z*z/2.0) + (y*y*z*z/3.0)); y = y * sqrtf(1.0 - (z*z/2.0) - (x*x/2.0) + (z*z*x*x/3.0)); z = z * sqrtf(1.0 - (x*x/2.0) - (y*y/2.0) + (x*x*y*y/3.0));

My sphere looks like this:

after

As you can see, the edges of the cube still poke out too far. The cube ranges from -1 to +1 on all axes, like the article says.

Any ideas what is wrong?

\$\endgroup\$
4
  • 1
    \$\begingroup\$ Does your implementation contain "x = x ..." problem too or is it just here? \$\endgroup\$ Commented Nov 14, 2012 at 9:55
  • 8
    \$\begingroup\$ Fantastic visual aids. Thankyou for including those. \$\endgroup\$ Commented Nov 14, 2012 at 10:04
  • 2
    \$\begingroup\$ To answer the question in the title, you can just normalize the vertices of the cube to make it a sphere. The distribution of the vertices will probably be different from the linked method though. \$\endgroup\$ Commented Nov 14, 2012 at 10:09
  • \$\begingroup\$ Related: gamedev.stackexchange.com/questions/7189/… \$\endgroup\$ Commented Nov 14, 2012 at 16:16

1 Answer 1

Reset to default
28
\$\begingroup\$

You've miswritten the formula.

x = x * sqrtf(1.0 - (y*y/2.0) - (z*z/2.0) + (y*y*z*z/3.0)); y = y * sqrtf(1.0 - (z*z/2.0) - (x*x/2.0) + (z*z*x*x/3.0)); z = z * sqrtf(1.0 - (x*x/2.0) - (y*y/2.0) + (x*x*y*y/3.0));

You modify the original x and overwrite it. Then you modify y based not on the original x but the modified x. Then you modify z based on the modified version of both of those.

Preserve the originals, and calculate this:

float dx = x * sqrtf(1.0 - (y*y/2.0) - (z*z/2.0) + (y*y*z*z/3.0)); float dy = y * sqrtf(1.0 - (z*z/2.0) - (x*x/2.0) + (z*z*x*x/3.0)); float dz = z * sqrtf(1.0 - (x*x/2.0) - (y*y/2.0) + (x*x*y*y/3.0));

Use dx, dy and dz from then on.

\$\endgroup\$
2
  • \$\begingroup\$ Whoops. Wasn't thinking. \$\endgroup\$ Commented Nov 14, 2012 at 10:15
  • \$\begingroup\$ do u have any sample source for the above program? \$\endgroup\$ Commented Dec 8, 2015 at 6:43

You must log in to answer this question.

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.