So I have very little experience in Mathematica but would like to learn how to plot. I have seen a few threads on this for $2\times 2$ systems but not for $3\times 3$.
So I'm trying to plot the phase portrait of the solution to the following equation:
$$\begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}'=\begin{pmatrix}-2&1&0\\1&-2&1\\0&1&-2\end{pmatrix}\begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}$$
To make matters easier, I found a general solution:
$$\begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}=c_1e^{2t}\begin{bmatrix}1\\0\\-1\end{bmatrix}+c_2e^{(2-\sqrt2)t}\begin{bmatrix}1\\-\sqrt2\\1\end{bmatrix}+c_3e^{(2+\sqrt 2)t}\begin{bmatrix}1\\\sqrt2\\1\end{bmatrix}$$
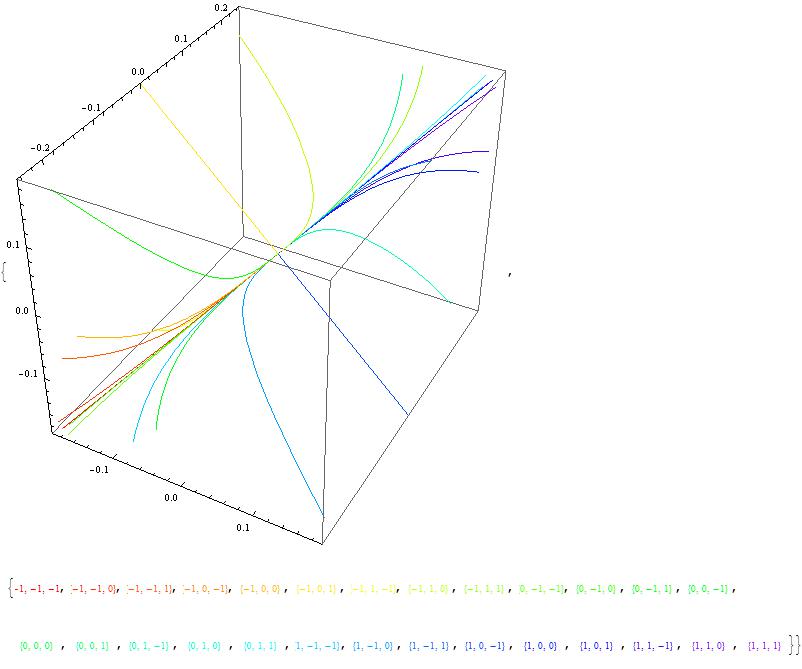
I considered $c_1=c_2=c_3=1$ and tried to plot a solution using the following with ParametricPlot3D:
ParametricPlot3D[{ E^(-2 u) + E^(-2 u + u Sqrt[2]) + E^(-2 u - u Sqrt[2]), Sqrt[2] E^(-2 u + u Sqrt[2]) - Sqrt[2] E^(-2 u - u Sqrt[2]), -E^(-2 u) + E^(-2 u + u Sqrt[2]) - E^(-2 u - u Sqrt[2])}, {u, -1, 10}, PlotTheme -> "Marketing"] I get a nice solution curve based on a single initial condition, but is there a nice way to plot many general solutions together?