I have two 2-D matrices $A$ and $B$(owns same dimentions) which have the style written as below:
$ \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1k} &\cdots &\cdots & a_{1,2k+1}\\ a_{21} & a_{22} & \cdots & a_{2k} &\cdots &\cdots & a_{2,2k+1}\\ \vdots & \vdots & \vdots & \vdots &\vdots &\cdots & \vdots \\ a_{k1} & a_{k2} & \cdots & a_{kk} &\cdots &\cdots & a_{k,2k+1}\\ a_{k+1,1} & a_{k+1,2} & \cdots & a_{k+1,k+1} & a_{k+1,k+1} &\cdots a_{k+1,2k} & a_{k+1,,2k+1}\\ a_{k+2,1} & a_{k+2,2} & \cdots & a_{k+2,k} &\cdots &\cdots & a_{k+2,,2k+1}\\ \vdots & \vdots & \vdots & \vdots &\vdots & \vdots \\ a_{2k+1,1} & a_{2k+1,2} & \cdots & a_{2k+1,k} &\cdots &\cdots & a_{2k+1,2k+1}\\ \end{bmatrix} _{2k+1\times 2k+1} $
Now I want to swap the value of some positions betwen them
My awkward solution
Edit Thanks for @Kuba
swap[a_, b_] := Module[{k, A = a, B = b}, k = Quotient[Length@A, 2]; {A[[1 ;; k, 1 ;; k]], B[[1 ;; k, 1 ;; k]]} = {B[[1 ;; k, 1 ;; k]], A[[1 ;; k, 1 ;; k]]}; {A[[k + 2 ;; 2 k + 1, 1 ;; k]], B[[k + 2 ;; 2 k + 1, 1 ;; k]]} = {B[[k + 2 ;; 2 k + 1, 1 ;; k]], A[[k + 2 ;; 2 k + 1, 1 ;; k]]}; {A[[k + 1, k + 1 ;; 2 k]], B[[k + 1, k + 1 ;; 2 k]]} = {B[[k + 1, k + 1 ;; 2 k]], A[[k + 1, k + 1 ;; 2 k]]}; {A, B} ] Test
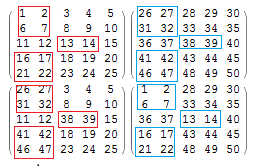
mat1 = Partition[Range[1, 25], 5]; mat2 = Partition[Range[26, 50], 5]; MatrixForm /@ {mat1, mat2} MatrixForm /@ swap[mat1, mat2] In addition, I have a trial to refactor the code
{A[[1 ;; k, 1 ;; k]], B[[1 ;; k, 1 ;; k]]} = {B[[1 ;; k, 1 ;; k]], A[[1 ;; k, 1 ;; k]]}; {A[[k + 2 ;; 2 k + 1, 1 ;; k]], B[[k + 2 ;; 2 k + 1, 1 ;; k]]} = {B[[k + 2 ;; 2 k + 1, 1 ;; k]], A[[k + 2 ;; 2 k + 1, 1 ;; k]]}; to the below style
{A[[{1 ;; k, k + 2 ;; 2 k + 1}, 1 ;; k]], B[[{1 ;; k, k + 2 ;; 2 k + 1}, 1 ;; k]]} = {B[[{1 ;; k, k + 2 ;; 2 k + 1}, 1 ;; k]], A[[{1 ;; k, k + 2 ;; 2 k + 1}, 1 ;; k]]} However, I failed in this trial and it seems that Span(;;) doesn't own this usage.
Question
- Is there other better methods(solutions) to implement this swap operation?