26
$\begingroup$

Does some package exist with a function that takes a parameter $n$ and generates a random 2D $n$-sided simple polygon (convex or non-convex), possibly within a certain bounding box?

It does not suffice to simply generate $n$ random points as I would have to figure out how to connect the points in a non-intersecting manner. I am sure there are algorithms to solve this particular problem, but I would much rather use a ready-made function that would be guaranteed to work, rather than code my own function and introduce more bugs.

I am trying to generate a large number of "random" test cases for my algorithm that is supposed to work for all polygons.

Improve this question
$\endgroup$
7
  • $\begingroup$ Without more information I'd put my money on RandomReal or similar. Please add as much info as possible and any relevant code you already have in place. $\endgroup$ Commented Sep 21, 2013 at 6:42
  • $\begingroup$ as @YvesKlett said, maybe: Graphics@Polygon[RandomReal[{5, 10}, {RandomInteger[{2, 10}], 2}]] or similar? $\endgroup$ Commented Sep 21, 2013 at 6:51
  • $\begingroup$ Generating a random cyclic graph - which is the limit of what RandomReal or RandomInteger can do - might yield a self-intersecting polygon, which I wish to avoid. I have elaborated on that in my edit to the question. $\endgroup$ Commented Sep 21, 2013 at 7:13
  • $\begingroup$ Can it have concave angles? $\endgroup$ Commented Sep 21, 2013 at 7:13
  • $\begingroup$ Yes, that is allowed, and desired. The question did not exclude such a possibility, and "randomness" would definitely produce some concave angles, but let me edit this into the question just to be safe. $\endgroup$ Commented Sep 21, 2013 at 7:18

4 Answers 4

Reset to default
16
$\begingroup$

There is some undocumented functionality in Graphics`Mesh that may help.

  • SimplePolygonPartition will break apart a self-intersecting polygon into non-self-intersecting components (the components include the "holes" in the original)
  • PolygonCombine will merge those components into a single polygon (note that while free of interior holes this polygon may still intersect itself)
  • FindIntersections will find any self-intersections and can therefore be used to filter out such polygons

.

Graphics`Mesh`MeshInit[]; randompoly := Module[{poly}, While[Length[FindIntersections[ poly = PolygonCombine @ SimplePolygonPartition @ Polygon[RandomReal[{-1, 1}, {25, 2}]]]] > 0]; poly] Graphics[{EdgeForm[Red], Yellow, randompoly}]

enter image description here

There are also some built-in polygons which may be useful for testing. They are:

PolygonData[] (* {"Blob", "ChvatalComb", "FractalCross", "HeptaSpiral", "HexaSpiral", "LSystem01", "PentaSpiral", "RandomWalk", "Test01", "TriSpiral"} *)

The available properties are:

PolygonData["Properties"] (* {"Data", "Graphics", "GraphicsLine", "GraphicsPoint", "GraphicsPolygon", "Line", "MeshObject", "Point", "Polygon"} *)

For example

polys = PolygonData[#, "Polygon"] & /@ PolygonData[]; Graphics[{EdgeForm[Red], Yellow, #}, ImageSize -> 100] & /@ polys

enter image description here

Improve this answer
$\endgroup$
5
  • $\begingroup$ I have tested your code and it works, but the output of randompoly is not a list poly = {pt1, ..., ptn} of 2D coordinates, but a graphics primitive Polygon[poly]. This hinders manipulation of the output polygon, unless there is a way to "unwrap" the raw data from Polygon? $\endgroup$ Commented Sep 22, 2013 at 3:08
  • $\begingroup$ the output polygons of randompoly also seem to have a "fat center" as compared to the output of @ybeltukov's answer. But I see this as a minor issue. $\endgroup$ Commented Sep 22, 2013 at 3:47
  • $\begingroup$ @HerngYi you can extract the coordinates using List @@ randompoly $\endgroup$ Commented Sep 22, 2013 at 4:23
  • $\begingroup$ Sorry but I couldn't find the documentation on the @@ operator - does it do something like replacing the header of an expression? Would be great if you could link me to some documentation on this. $\endgroup$ Commented Sep 22, 2013 at 5:21
  • 1
    $\begingroup$ @HerngYi Yes, that's exactly what it does. You can select @@ in the Front End and press F1 key to bring up the page for Apply. You could also use this reference to find the same page. $\endgroup$ Commented Sep 22, 2013 at 7:43
20
$\begingroup$

I propose "deintersection" algorithm.

Let we have $n$ random points.

n = 10; p = RandomReal[1.0, {n, 2}];

We want change the order of this points to get rid of the intersections.

Line segments $(p_1,p_2)$ and $(p_3,p_4)$ intersect if and only if the signs of areas of triangles $p_1p_2p_3$ and $p_1p_2p_4$ are different and the signs of areas of triangles $p_3p_4p_1$ and $p_3p_4p_1$ are also different.

enter image description here

Corresponding function

SignedArea[p1_, p2_, p3_] := 0.5 (#1[[2]] #2[[1]] - #1[[1]] #2[[2]]) &[p2 - p1, p3 - p1]; IntersectionQ[p1_, p2_, p3_, p4_] := SignedArea[p1, p2, p3] SignedArea[p1, p2, p4] < 0 && SignedArea[p3, p4, p1] SignedArea[p3, p4, p2] < 0;

Main step

enter image description here

Patterns in Mathematica are very convenient for the searching and removing intersections. 

Deintersect[p_] := Append[p, p[[1]]] //. {s1___, p1_, p2_, s2___, p3_, p4_, s3___} /; IntersectionQ[p1, p2, p3, p4] :> ({s1, p1, p3, Sequence @@ Reverse@{s2}, p2, p4, s3}) // Most;

To add the segment between the last and the first point I use Append and Most.

As a result we got the polygon without intersections

p2 = Deintersect[p]; Graphics[{Lighter@Red, EdgeForm@Thickness[0.01], EdgeForm@Red, Polygon[p2]}]

enter image description here

And many other funny polygons

Graphics[{Lighter@Red, EdgeForm@Thickness[0.01], EdgeForm@Red, Polygon[#]}, ImageSize -> 100] &@Deintersect[#] & /@ RandomReal[1.0, {10, n, 2}]

enter image description here

As you can see, this algorithm can give more complicated polygons than in other answers.

Improve this answer
$\endgroup$
2
  • $\begingroup$ This is the same idea I had after reading the question but I wasn't sure how to go about it. Good thing you're here to implement it for us. :-) +1 $\endgroup$ Commented Sep 22, 2013 at 7:45
  • $\begingroup$ I like the elegance of the implementation using patterns, and the assortment of generated polygons seems more random than that of the other answers, but I was looking for a ready-made function, not a new algorithm. I think that others who ask the same question will be looking for ready-made functions as well, so I did not accept this answer. I will use both this answer and that of @SimonWoods' in my testing, though. $\endgroup$ Commented Sep 22, 2013 at 10:41
13
$\begingroup$

======= update ===========

I guess a general method (to get elongated polygons too) would be to sample elliptic shapes of various axis ratios at a few points and then perturb them outwards (inflate) randomly.

ngon[n_, s_, r_] := Polygon[RandomReal[r, n] Table[{s Cos[2 Pi k/n], Sin[2 Pi k/n]/s}, {k, n}]] Table[ngon[RandomInteger[{7, 13}], RandomInteger[{1, 3}], RandomReal[{1, 2}]] // Graphics, {5}, {5}] // GraphicsGrid

enter image description here

======= older ===========

Maybe this post is useful to read - there is some sorting points discussion:

Character edge finding

Another idea that does it in a simple way is a perturbative approach. Start from a regular polygon and randomly perturb the vertices. Note it will keep polygons within some bounding box defined by regular polygon side and max perturbation amplitude.

For positive-negative perturbations smaller than some number self-intersections will be impossible. For another positive only perturbations and a different "smaller than number" you will have only convex polygons. The value of these "smaller than numbers" can be found from geometric considerations that I leave to you.

For arbitrary concave and convex shapes define:

ngon[n_, r_] := Polygon[Table[RandomReal[{-r, r}, 2] + {Cos[2 Pi k/n], Sin[2 Pi k/n]}, {k, n}]] Table[Graphics[ngon[RandomInteger[{3, 9}], RandomReal[{.3, .7}]]], {5}, {5}] // GraphicsGrid

enter image description here

Here is the limiting case of perturbing a line:

n = 7; pts = Table[k/n, {k, -n/2, n/2}]; Table[Join[{RandomReal[{1.1, 1.5}] #, RandomReal[{0, .2}]} & /@ pts, {RandomReal[{1.1, 1.5}] #, RandomReal[{0, -.2}]} & /@ pts // Reverse] // Polygon // Graphics, {5}, {5}] // GraphicsGrid

enter image description here

For shapes only convex (with another "less than" parameter):

ngon[n_, r_] := Polygon[Table[RandomReal[r, 2] + {Cos[2 Pi k/n], Sin[2 Pi k/n]}, {k, n}]] Table[Graphics[ngon[RandomInteger[{3, 9}], RandomReal[{.3, .4}]]], {5}, {5}] // GraphicsGrid

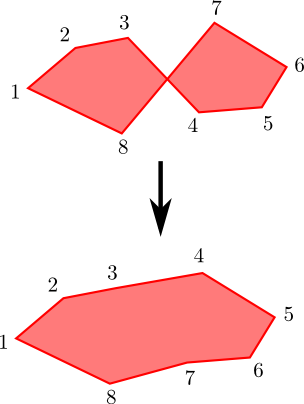
enter image description here

Improve this answer
$\endgroup$
4
  • $\begingroup$ Perturbation under a small displacement limit will not be able to produce "thin" polygons such as slightly thickened graphs. I need to test my algorithms on those kinds of polygons as well. $\endgroup$ Commented Sep 21, 2013 at 8:55
  • $\begingroup$ @HerngYi those can be simulated by perturbing an infinitely thin loop (line) with random shifts outwards from geometrical center. $\endgroup$ Commented Sep 21, 2013 at 9:06
  • $\begingroup$ @HerngYi I modified the method to get all types. See update. $\endgroup$ Commented Sep 21, 2013 at 9:48
  • $\begingroup$ This is still a rather limited variety - You may be able to produce "thickened lines" but not a general "thickened tree", for example. $\endgroup$ Commented Sep 21, 2013 at 10:10
9
$\begingroup$

From V12, there is an inbuilt function RandomPolygon

RandomPolygon[7] returns a simple polygon with seven sides. Other types are "Convex", "StarShaped".

Table[Graphics[p, ImageSize -> 100], {p, RandomPolygon[{"Simple", 5}, 3]}], Table[Graphics[p, ImageSize -> 100], {p, RandomPolygon[{"Convex", 5}, 3]}], Table[Graphics[p, ImageSize -> 100], {p, RandomPolygon[{"StarShaped"}, 3]}]}]

enter image description here

In general RandomPolygon[{"Convex", 5}, 3, DataRange -> {{1,2}, {3,4}}] would give you 3 random pentagon within the rectangular box (1,3) to (2,4).

Improve this answer
$\endgroup$

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.